ABSTRACT
In the first part of this article I will speak about magnitudes, probabilities, and entropy, proposing to use a different expression to indicate entropy: expected length of code. The first part of the article is in preparation for the second part, in which I will give a simplified description of the concept of Complexity as introduced by Gerald Edelman and of the concept of PHI, proposed by Giulio Tononi in the context of integrated information theory. In this article PHI is presented as an interesting parameter, not as the core property of consciousness. The main mathematical reference that I employed for PHI is the work of Barnett, Barrett, Seth et al.
PART I: ENTROPY AS EXPECTED LENGTH OF CODE
I.THINGS WE CAN MEASURE
II.KOLMOGOROV AND INTROSPECTION
III.A CERTAIN BLINDNESS
IV.DIVIDING THE WORLD; CLASSICAL INTERPRETATION AND SAME WEIGHT CASES
V.MANAGING COMBINATIONS: LABELS, AND THE WORK OF LOGARITHM
VI.GENERALIZING THE SAME WEIGHT SCENARIO AND THE IDEA OF EXPECTED LENGTH OF CODE
VII.INFORMATION OR COMBINATIONS?
PART II: SAVED CODE AND CONSCIOUSNESS: TWO DIFFERENT BUSINESSES
I.EDELMAN AND COMPLEXITY
II.DESCRIBING A PHOTO: THE SAVING OF CODE
III.CONSIDERING TIME; THE METAPHOR OF THE FILM
IV.EFFECTIVE INFORMATION: THE ADVANTAGE OF THE WHOLE
V.CHECKING FOR INDEPENDENT STORIES – WHICH DECOMPOSITION?
VI.HOW MUCH THE WHOLE IS UPPER THE PARTS
VII.CONCLUSIONS: THE HACKER AND THE ELECTRICIAN
APPENDIX A: A SELECTIONIST ARGUMENT TO MAKE THE CASE FOR CONSCIENT MATTER
APPENDIX B: SOME GRAMMATICAL ISSUES
PART I: ENTROPY AS EXPECTED LENGTH OF CODE
I. THINGS WE CAN MEASURE
Measuring is assigning numbers to objects to represent their properties, but this assignment isn’t simply labelling, like the numbers on the t-shirts of football players, there must be some mathematical property of these numbers that represents relations among those objects.[1] A common example is addition. Think of five random physical objects. Each of them has a weight, we can put them in order from the lightest to the heaviest, and if we add one kilogram to each of these items, their order won’t change. These are some basic facts related to weight having an additive property.
Let’s think of a counterexample in order to fix our ideas. If we take five different pictures it is not possible to find an objective disposition of them from the ugliest to the most attractive, and even if we find it, it’s not possible to add another picture to each of the five initial ones, wielding five new pictures with the same order of beauty.
Maybe we can imagine some particular cases and find certain sequences for certain images that satisfy the conditions according to our taste, but with weight we are able to manage every kind of object in the same way, always obtaining the same results valid for everyone, everywhere.
The objects of measuring are those properties called magnitudes or quantities. Magnitudes are something more similar to real numbers than natural numbers, and, according to Gallistel, the ability to manage them is a very deep and ancient property specific to the mind of men and animals.[2]
II. INTROSPECTION AND KOLMOGOROV
The world produced the mind both with the events of our lives and by the evolutionary history of our species. We host many different weights of likelihood assigned to different items of the world. We are a sort of experiment that harvests the marks of the repetitions of past generations. In the past we stored in our warehouses the structures of many series and now we reproduce and compose them to accomplish our daily tasks. Maybe we will find that there is some property of DNA that facilitates these harvesting activities, and we will realize that there should be a moment in the ancient past when this property was selected.
When we develop a representation and we ask ourselves what is the chance this is true of a certain part of the world, then our mind collects the weight of these items that the representation is made of, and composing them it allows us to assign a certain truth weight to the whole representation. This is what introspection and intuition tell us about probabilities and these weights can be thought of as magnitudes.
Since they are magnitudes, we are able to compare different probabilities and to make additions out of them, even if with just a certain approximation. For example, we can compare the probability of a red number at the roulette and estimate it is larger than the probability of the numbers 3 or 4 over a single throw of the dice. We can operate over probabilities as we operate over weights and lengths, treating them as measurable items.
Not only intuition pushes us to consider probabilities as magnitudes. When it comes to get a formal definition of probabilities the main reference is the work of Kolmogorov. He asked that probabilities, in addition to being non-negative and having a total amount of 1 (normalization), also to being subject to addition.[3] The definition of Kolmogorov establishes probabilities essentially as something that can be measured, making them of the same breed of magnitudes.[4]
III. A CERTAIN BLINDNESS
By probabilities we can treat as magnitudes a great extent of the phenomena in the world, so that in a sense we can think about probabilities as a translation from shapes to magnitudes, as a numerification of the shape. In this conversion some part of information is lost, and a knowledge made of probabilities is affected by a certain blindness in respect to what we could call a knowledge made of structure. Here is an example.
Let’s imagine a solid block with an entrance on the top where we can put a ball. Inside the block there is a web of tunnels ending in 10 holes on the bottom side, and under each bottom hole there is a box. If we are asked to build probabilities about the boxes where the ball will fall, the first move could be to give each box the same chance of 10%. If we are allowed to put the ball in the block one hundred times and check the results, we will understand that the ball dropping into certain boxes is more likely and we will shape our probabilities accordingly. If we are allowed to make the same experiment many more times we will be able to further refine our set of probabilities, but we will never get the same knowledge that we would get opening the block. Instead, if we know how the web of tunnels is made, and if we have enough knowledge about physics, we will be able to build an exact and definitive attribution of probabilities. If we know the structure of the block we can write its probabilitities, but if we know its probabilities we can not describe its structure.
At the beginning of the previous chapter I considered knowledge equivalent to a structure of frequencies, while here I pose knowledge in opposition to a structure of frequencies. The difference is that in the previous case I was talking about the whole structure of frequencies constituting the past of our species and of ourselves, while here I’m talking about the structure of frequencies of a single experiment over a single object. In the previous case, the issue was the rising of our intelligence, while here an already established intelligence is operating to build a description of a circumscribed item.
IV. DIVIDING THE WORLD; CLASSICAL INTERPRETATION AND SAME WEIGHT CASES
When we want to foresee the future, we can try to describe a series of possible outcomes, each with the same probability. This is the core idea behind the classical interpretation of probabilities. The primitive capacity required from our mind to accomplish this task is that of dividing the world into possible states or events. We find this issue also at the beginning of the work of Kolmogorov, who posits as a primitive object a collection of possible events: probabilities come only after the definition of the items to which we apply them.
It is our knowledge that allows us to divide the world into different states and events, and if we consider ourselves as the imprint of the frequencies of the world, then it is from this imprint that derives our ability to divide the world into objects and landscapes.[5] If often we do this well, this testifies to the good work carried out by evolution upon our minds, but there is no guarantee of a successful outcome to this process. We have to divide the world, but we don’t know in advance the best division, and different assignments of probabilities are possible. About this issue, it is interesting to consider the Bertrand’s Paradox in this version: “A factory produces cubes with side-length between 0 and 1 foot; what is the probability that a randomly chosen cube has side-length between 0 and 1/2 a foot? The tempting answer is 1/2, as we imagine a process of production that is uniformly distributed over side-length. But the question could have been given an equivalent restatement: a factory produces cubes with face-area between 0 and 1 square-feet; what is the probability that a randomly chosen cube has face-area between 0 and 1/4 square-feet? Now the tempting answer is 1/4, as we imagine a process of production that is uniformly distributed over face-area.”[6]
I reported this example to show a clear situation where we can’t jump over our doubts about the assignment of probabilities only by reasoning, without going to check what is happening in the world. Our representations do not retain the whole truth of the world for obvious reasons, because we only receive the content of senses, because memory deteriorates and it is never as complete as the current input of senses, and because of the cognitive work made by the cortex. Our representations are naturally made by dropping certain parts of the world. As a consequence, it would be quite strange to be able to accomplish a correct attribution of probabilities “a priori”, only relying on reflection over representations, without probing into the world. Dropping allows us to manage thinner thoughts and makes it possible to have more daring representations, but then we need to go back into the world to verify them.
It seems that the idea of same weight cases is not related with the intimate nature of the world, which we don’t know if we can grasp. It seems to be only one of the strategies to develop our ever evolving approximation of the world. Nonetheless, it remains an important reference for its simplicity. In fact, when we are in a situation of same weight cases, the probability of each case is the inverse ratio of the number of cases. For example, the number of cases after throwing a die is 6, and each of them results in the same probability = 1/6.
V. MANAGING COMBINATIONS: LABELS, AND THE WORK OF LOGARITHM
For managing cases we need to assign a label to each of them. Labelling is a basic form of description where we have a one-to-one relation among the described items and the words of which our description is made. To represent a certain number of cases we need a string that can give us at least that same number of combinations.[7]
If we have a set of, say, 4 characters, each of which can assume 10 different values (from 0 to 9), then the number of ordered combinations is 10 x 10 x 10 x 10, that we can write also as 104 = 10.000 = the number of combinations from 0000 to 9999. Power gives us to the number of possible combinations starting from the number of the characters that we can use. Logarithm works out the opposite function: given the number of different combinations, it returns us the number of characters needed to express them, which is a length of code. For example, if we have to label 100 products we will need two numbers, using all the combinations from 00 to 99. Similarly, if we have 1000 products, then we will need 3 numbers. If there are 2600 products, then we will need 4 numbers, the first which is used only in part. This partial use is reflected in the decimal value of the logarithm of 2600, which is 3,41.
In the instance of same weight cases, as we saw in the previous chapter, the number of cases is given by the inverse ratio of probability, and if we apply the logarithm to this quantity, then we get the length of code needed to label the number of cases that we are considering.
VI. GENERALIZING THE SAME WEIGHT SCENARIO AND THE IDEA OF EXPECTED LENGTH OF CODE
If we list all the possible states of a certain part of the world and we assign them probabilities, then we have a set of probabilities. For a certain set of probabilities, entropy is defined as the sum of the logarithms of 1/p, weighted by p: ∑ p log (1/p). The interpretation of 1/p as a number of possible cases allows us to consider its logarithm as a length of code, and the overall sum of the possible values weighed by p is, by definition, its expected value. So this sum is the expected length of code[8] required to label all the cases related to a certain set of probabilities. This interpretation is straightforward in the instance of same weight cases, but we need to extend it to the general circumstance when different cases have different weights.
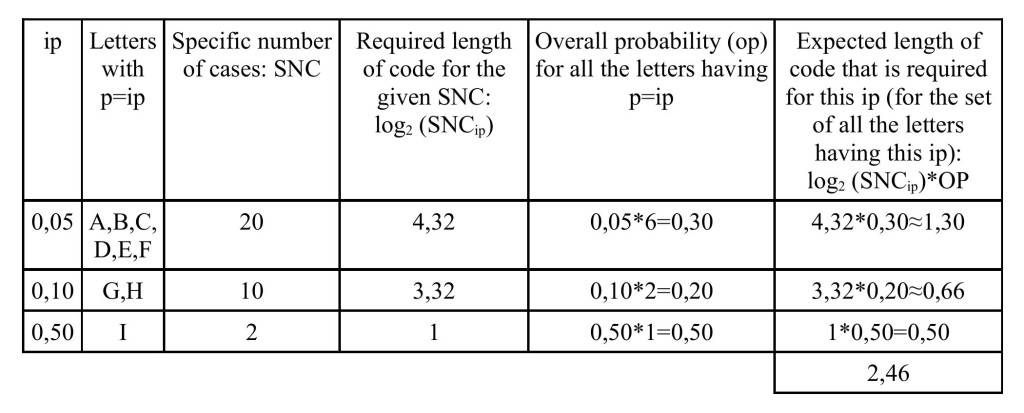
In order to do this we have to break up the situation into subgroups where all configurations have the same probability ip (where ip stands for individual probability). Let’s make an example: suppose we have a book made of the letters A,B,C,D,E,F,G,H,I. Every character of the book takes values according to the following probabilities:
the probability of A is 0,05 (one twentieth)
the probability of B is 0,05 (one twentieth)
the probability of C is 0,05 (one twentieth)
the probability of D is 0,05 (one twentieth)
the probability of E is 0,05 (one twentieth)
the probability of F is 0,05 (one twentieth)
the probability of G is 0,10 (one tenth)
the probability of H is 0,10 (one tenth)
the probability of I is 0,50 (one half)
The value assumed by each character is independent of the preceeding ones. Thus, the part of the book assuming a configuration with individual probability 0,05 is given by the sum of the probabilities equal to 0,05, that is (0,05+0,05+0,05+0,05+0,05+0,05)=0,30. In a similar way, the part of the book assuming a configuration with individual probability 0,10 is (0,10+0,10)=0,20.
For the part of the book assuming a configuration with individual probability 0,05, the specific number of possible cases is twenty. We define this number as the number of possible cases if the portion characterized by a certain individual probability would be 100% of the system that we are considering. We can also think of it as the number of possible cases divided by the related fraction of this system.[9] This implies that we use this term qualitatively, not quantitatively.
Thus, dealing with configurations characterized by a certain individual probability ip, the length of code required to label the possible cases is the logarithm of the specific number of possible cases. This value is then weighed by multiplying it with the part of the system that assumes configurations with that individual ip, which we call the overall probability (op) of that individual ip.
In this way we get all the contributions for the expected length of code, which are in the last column of the table above. Making a sum over the items of this column we get entropy, and we see it as the expected length of code needed to label all the possible outcomes for each character of the book. Since in these paragraphs we worked with the logarithm in base 2, we get this measure of code in bits; we need 2,46 bits to represent each character of the book.
Of course, these operations are the same that we usually make to calculate entropy, only the grouping is different.[10] The essence of entropy is absolutely untouched by this recasting, which is intended only to give intuition a different way to understand the structure behind this concept, and to support the renaming of this quantity.[11]
VII. INFORMATION OR COMBINATIONS?
Entropy is higher for a disturbed screen than for a film, and this does not fit our idea of information: who thinks that the disturbance has a higher level of information? Entropy is not a measure of information. It seems safer to follow the reasoning just exposed, conceiving it as a measure of a number of combinations and of the length of code needed to generate them.
Combinations can turn into information, but they are not information in and of themselves. They become information only interacting with the mind. These considerations agree with the idea of Searle that “information is in the eye of the beholder.”[12]
We could even say that information is in the eye of the beholder twice. Once in the sense of Searle, because a mind produces information adding the content of terms, which are retrieved from its inner warehouses, to combinations. But before this can happen, we need the premises for combinations to exist: the mind must identify the basic elements that we can use to compose combinations.
PART II: SAVED CODE AND CONSCIOUSNESS: TWO DIFFERENT BUSINESSES
I. EDELMAN AND COMPLEXITY
Gerald Edelman won a Nobel prize for his description of antibodies by selectionism; he is also famous for a selectionist interpretation of the neural structures of the mind.[13] In 1994 he published an article together with Tononi and Sporns[14], trying to grasp with a formula some important traits of the higher living beings, namely the coexistence of functional segregation and functional integration. Integration and segregation are intended respectively as dependence and independence, and thus they are naturally present in every system. In living beings we can find a strong integration at the global level, and the aim of these scientists was to find an exact quantity, which then they called Complexity, related to this trait. In order to do this, they examined dependence and independence over neural networks by using the concept of entropy. In the following paragraphs I will try to describe the core of their theory with some images, avoiding technical terms, and using the concept of code instead of entropy.
II. DESCRIBING A PHOTO: THE SAVING OF CODE
Think about a web of neurons the states of which are numbers. The set of all these numbers is the description of the web; we can imagine it to be a digital photo in which the pixels are the states. Think of a man dressed in black, doing various phisical actions in a white room. We are photographing at him. In each photo there is a wide area made of white or light grey shades, and darker colors making up the figure of the man. If we have to describe the photo pixel by pixel we will have no other possibility than to tell the color of each pixel. But if we consider wider zones of the image we will be able to describe a black zone by only giving its perimeter, without repeating that each pixel is black. This is the main point: considering wider zones we can create a shorter description for the same image and we get a certain amount of saved code. The more the pixels are interdependent, the larger integration is and the saving of code when the pixels are considered together. We can use this amount of saved code as a measure of interdependence; the usual expression for this concept is mutual information. This is defined as the sum of the expected lengths of code[15] for the distinct elements, minus the expected length of code for all these basics elements considered together.[16]
The last step is considering the system at different scales. The basic expectation for whatever a system is that the saving increases linearly with the size of the system. Instead, if we see that the saving (and thus integration) increases more than linearly with size, we have Complexity.[17]
III. CONSIDERING TIME; THE METAPHOR OF THE FILM
Some year later the conception of Complexity, the way of Tononi departed from that of Edelman. He proposed a different measure, PHI, in the context of what he called integrated information theory.[18] PHI is what we are going to talk about, referencing to the treatment given by Barrett, Barnett and Seth.[19]
In respect to the previous case we will need to consider the relationship among subsequent states, moving our analysis into time. Thus, instead of the metaphor of the photo we will employ the metaphor of the film. We will find again the concept of integration, but its implementation will be different.
Think again about the web of neurons, which now changes its state 1000 times every second. Given the state of the web at a certain time, this will influence the state of the web in the following steps. If we want to describe the state of the web at a certain point in time we will need a certain amount of code; if we want to describe it starting from the knowledge of the previous states, we will need less code. If we are shooting a film of the black dressed man of the previous paragraphs we can avoid to describe the whole frame, we can only describe the differences in respect to the former. So, this time too we have a certain amount of saved code, when we can describe the present on the basis of the past. This fact is related with the stuff that present and past have in common.
IV. EFFECTIVE INFORMATION: THE ADVANTAGE OF THE WHOLE
Break the screen into 4 x 4 = 16 little screens. For each of them we can calculate the amount of code that we can save once we know its prior state. However, if we add together all these 16 little savings we get an overall saving that is less than the saving that we get when we consider the whole screen. In fact, when we consider the whole screen we are be able to detect the arm of the black dressed man moving from the top of the screen to the lower part, and so we are able to predict that the lower part of the screen is going to display the color of the sleeve of our man. Instead, if we consider independently each of the 16 screens, we are not able to exploit what is happening in the other parts of the screen to improve our prediction about the content of the little screen currently under examination.[20]
We can obtain a saving of code from the knowledge of the past and this saving is bigger when we consider the whole screen instead of the single little screens independently. The increasing of the saving that we get when we consider the whole screen in respect to the 16 little screens independently is called effective information. Effective information is the saving of code due to the consideration of the whole system in respect to its parts, in a context where we take into account the development into time.
The expression ‘effective information’ indicates that considering the system as a whole we can grasp a certain amount of information that we could not grasp considering only its parts, and that this information is useful to determine the future states of the system. Thus, in a certain sense, this information has an effect over the future system.
The difference between integration and effective information lies in the former being a general idea and the latter being a precise measure that tries to better define the former in the context of a well defined mathematical model.[21]
V. CHECKING FOR INDEPENDENT STORIES – WHICH DECOMPOSITION?
Now think of this example: we have a film, and for its entire duration the frames are divided into 2×2=4 screens. In each one a completely different story is going on with completely different characters. The saving of code we get considering the whole screen is a maximum, of course, but we can get the same saving also considering the 4 screens independently. This is the same as saying that the whole screen doesn’t show a greater integration in respect to the 4 screens. In this situation the overall system ends to lose some of its privilege of uniqueness, grant that our aim is the individuation of the states with the greatest integration.
If we now stop thinking about the film and we go back to considering the web of neurons, how can we be sure that what is going on is a unique coherent film and not 4 distinct stories? When we deal with the video we can literally understand at a glance what is going on, but when we deal with a web of neurons we don’t know which could be the subset of the web, having its own behaviour independent from the rest. We can’t consider only adjacent items as the pixels of each of the four screens. We have to consider all the possible divisions of the web, also taking into account the relations among distant neurons. This is where calculations become resource demanding.[22]
VI. HOW MUCH THE WHOLE IS ABOVE THE PARTS
The parts generated by every decomposition of the web need a certain amount of code to be described, which is complexively higher than the amount of code needed when we consider the system as a whole. The decomposition that needs the smallest amount of code to be described is the one with the major integration; if we consider the system as a whole we will only get a little saving in respect to it. Tononi set up the convention to consider the smallest saving of this kind as a measure of consciousness and called it PHI. In other words, he managed to find a quantity that is bigger when the level of integration of all the decompositions is lower in respect to the whole system. This means that there are many causes and effects that can be understood only by considering the system as a whole.
For example, in the film described at the beginning of chapter V, there is a decomposition (that of the 4 little screens) preserving the same level of integration of the whole. In this case PHI is zero, and in a certain sense there is no need to consider the current system as a whole.
VII. CONCLUSIONS: THE HACKER AND THE ELECTRICIAN
In this article I only gave a simplified description of a complex mathematical treatment. At the end of the story we have a quantity made up of bits telling us how much the work of our neurons is interdependent. PHI is an interesting parameter, a correlate of consciousness, as they say; it can be used in combination with other neurophysiological data to chase the properties of consciousness, but it is not the ultimate nature of consciousness. Tononi claimed too much about this.[23] Trying to understand consciousness by this measure is like trying to understand human activities by looking at the lights of a city in the night from a satellite. And there are too many dark rooms, the content of which we can’t see.
The statistical work about information integration can be inscribed in the cognitive course that employs the computer as the main metaphor of the mind. But there is not only one way to take inspiration from a computer. For example we can think that everything in the mind can be reduced into bits, or we can list all the input and the output of the mind, or we can go searching for the magical kernel of the software that runs the most important routines. Think of Jaak Panksepp, with his work on emotions. He deems the metaphor of the computer to be misleading when it comes to understanding the mind, but he is more similar than Tononi is to the hackers who sniff a secret system they don’t know, in order to understand its structure. On the other hand, what is the operation over the structure of a computer that is equivalent to the analysis by PHI? Maybe it is the approach of an electrician who tries to understand the functioning of a computer by the electrical properties of the items it is made of? Probably our electrician will be able to understand when the computer is turned on and when it’s carrying a heavy load, but maybe this is not the way we can understand software that we don’t know.
In the land of this science we are not citizens, we are travellers always thinking about our own home. What do we ask from knowledge about the mind? We need the keys to handle the day by day dancing battle that we carry on with the inner parts of ourself. The analysis of the overall interdependence among neurons can be used as a tool for brain imaging in an operating theatre, in order to understand if one is conscious, but it seems to not be useful in improving our skill in managing introspection, which is the main interface with ourselves.
APPENDIX A: A SELECTIONIST ARGUMENT TO MAKE THE CASE FOR CONSCIENT MATTER
Tononi claimed that PHI has a physical meaning and that where we have PHI we have consciousness. There was a debate between Tononi and Searle about this issue, and in this occasion Tononi’s thought was assimilated to a form of panpsychism.[24] I don’t agree with Tononi about the meaning of PHI, but there is still a possibility for consciousness to be a fundamental property of matter.
Let’s avoid the term consciousness for a while, and talk about these two concepts: 1) the capacity to manage the representations of the world in the broadest sense, and 2) the feeling that we exist. Let’s call them respectively representative skill and awareness. We are used to having these two properties together, but they are not the same thing. Awareness is what is missing in a zombie or in a computer simulation of the mind, even if this simulation were capable of reproducing all the tasks of thought, thus demonstrating to possess a full fledged representative skill.
It is acceptable to think that selection selects the representative skill during evolution, because this is useful to guide our bodies into the world, but what about awareness? Or we admit awareness as a fundamental property of the physical world, or we have to explain how it arose. If we accept the fact that selection is the only mechanism that could generate its arising, and that selection only chooses useful things, then explaining the arousal of awareness accounts for finding how it is useful; but I cannot see the usefulness of awareness. Of course the possibility remains that awareness arose as a collateral product of the devices underlying the representative skills, but still we would have to find the relation between awareness and these skills.
Let me make a science fiction game for a paragraph, thinking that maybe awareness is a property of the electromagnetic field, and that this field forms complex structures in neurons, while outside them only simpler objects are formed. Of course this is only a naive speculation. I make it only because a concrete example can help us in understanding the involved abstract terms, and because it can give us a hint for replying to the objection posed by Searle towards panpsychism, “Consciousness comes in units and panpsychism cannot specify the units.”[25] The expected length of code (entropy) and combinations need units, but consciousness maybe not, or at least no more than the quantum discretization.
We saw that since selection does not select items without effect, if awareness is useless we can’t get it by selection, and thus, since it exists, it must be a fundamental property of matter. But is this important? Two of humans’ main current problems as they are now are death and the division of different heads, which makes it difficult forming choruses. The fact that, say, a stone has a minimal amount of consciousness does not help us to fix either of these issues. The practical effect of knowing matter to be conscious is not so large, but this thought, if true, could contribute to determining a new important metaphor for understanding ourselves and the world.
APPENDIX B: SOME GRAMMATICAL ISSUES
According to Quine a general term is a term that “is true of each, severally, of any number of objects”; it is opposed to the singular term, which “purports to name just one object, though as complex or diffuse an object as you please.” There are then mass terms, that “like ‘water’, ‘footwear’, and ‘red’ have the semantical property of referring cumulatively: any sum of parts which are water is water.”[26]
We can use the word ‘code’ as a general term, as in the expressions ‘we need 1000 different codes to label these products’ or ‘this code is wrong’. But we can also use it as a mass term, perceiving it as a magnitude, like in the expression ‘quantity of code’. When we talk about ‘length of code’ the word ‘code’ is used as a mass term.[27] When in this article I talked of specific codes, I usually employed the word ‘combination’ instead of ‘code’, in order to avoid confusion. Sometimes I also used the word ‘label’ as a general term, both as a substantive and a verb.[28]
About the word ‘combination’: I used it intending to mean ordered combinations with repetitions, while in mathematics this word is used to indicate a sequence without order and without repetitions. I preferred to keep this word despite this counterindication, because it focuses on the discrete nature of the issue better than other terms like sequence, configuration, disposition or arrangement.
- [1]José A. Díez, “A Hundred Years of Numbers. An Historical Introduction to Measurement Theory 1887-1990,” Stud. Hist. Phil. Sci. 28, (1997): 167-185.↩
- [2]Charles R. Gallistel, Rochel Gelman, Sara Cordes, “The cultural and evolutionary history of real numbers.” In Evolution and Culture: A Fyssen Foundation Symposium, ed. S. Levinson & P. Jaisson (Cambridge, MA: MIT Press, 2006).↩
- [3]Andrey N. Kolmogorov, Foundations of the Theory of Probability (New York: Chelsea Publishing Company, 1956).↩
- [4]“Kolmogorov comments that infinite probability spaces are idealized models of real random processes, and that he limits himself arbitrarily to only those models that satisfy countable additivity. This axiom is the cornerstone of the assimilation of probability theory to measure theory. ”
Alan Hájek, “Interpretations of Probability,” The Stanford Encyclopedia of Philosophy, (Winter 2012 Edition), http://plato.stanford.edu/archives/win2012/entries/probability-interpret/↩ - [5]By the way, our structure of frequencies depends on the body it is based upon. If we see our body as a set of transducers, then we can ask ourself how much the specific set of transducers influences this structure of frequencies. We can also ask what will happen embedding new transducers in the body, and even if we can drop the body once the business of intelligence is established by means of that body.↩
- [6]Alan Hájek, “Interpretations of Probability,” The Stanford Encyclopedia of Philosophy, (Winter 2012 Edition), http://plato.stanford.edu/archives/win2012/entries/probability-interpret/↩
- [7]See appendix B for the use of the word ‘combination’.↩
- [8]In order to indicate this quantity we could also use the abbreviation ELOC.↩
- [9]In this case it is 6/0,30=20↩
- [10]The standard operations for calculating entropy in this case are: 6*(0,05*log(1/0,05) ) + 2*(0,10*log(1/0,10) + 1*(0,50*log(1/0,50).↩
- [11]In 1948, Shannon used the word ‘entropy’ to dub a quantity, the formula of which was the same of thermodynamic entropy. It is reported that Von Neumann suggested to Shannon that he should use the word ‘entropy’ because no one understood this concept very well.
Cf. Myron Tribus, Edward C. McIrvine, “Energy and Information,” Scientific American 225(3), (1971): 179-188.↩ - [12]John R. Searle, “Can Information Theory Explain Consciousness?” The New York Review of Books, January 10, 2013, http://www.nybooks.com/articles/archives/2013/jan/10/can-information-theory-explain-consciousness/↩
- [13]Gerald M. Edelman, Darwinismo Neurale. La teoria della selezione dei gruppi neuronali. (Neural Darwinism. The Theory of Neuronal Group Selection.) Torino: Einaudi, 1995.↩
- [14]Giulio Tononi, Olaf Sporns, and Gerald M. Edelman, “A Measure for Brain Complexity: Relating Functional Segregation and Integration in the Nervous System,” Proc. Natl. Acad. Sci. USA 91, (1994): 5033.↩
- [15]The use of the adjective ‘expected’ implies that we don’t know the content of the photo, and that we have to describe it probabilistically. For the sake of simplicity, and in order to focus on the core concepts that I want to illustrate, I often skip this conceptual step and instead I talk about exact images that we already know. The use of the expression ‘expected lenght of code’ allows us to do this overtly, dropping the adjective ‘expected’, while we can’t do this with the word ‘entropy’.↩
- [16]Compare these considerations to the following expression by Shannon about mutual information, referring to the expression H(x) + H(y) – H(x,y): “it is the sum of the two amounts less the joint entropy and therefore in a sense is the number of bits per second common to the two.” Claude E. Shannon, “A Mathematical Theory of Communication,” The Bell System Technical Journal 27, (1948): 379.↩
- [17]In order to keep a more complete parallelism between these images and the web of neurons as considered scientifically in the articles that I’m talking about, one shouldn’t simply consider the code needed to describe a certain image, but rather a method for describing a whole family of images. I avoided putting this consideration in the foreground for the sake of simplicity.↩
- [18]Giulio Tononi, “An Information Integration Theory of Consciousness,” BMC Neurosci 2004, 5:42, doi:10.1186/1471-2202-5-42↩
- [19]Anil K. Seth, Adam B. Barrett, Lionel Barnett, “Causal density and integrated information as measures of conscious level,” Phil. Trans. R. Soc. A 369 (2011): 3748–3767, doi:10.1098/rsta.2011.0079
Adam B. Barrett, Anil K. Seth, “Practical Measures of Integrated Information for Time-Series Data,” PLoS Comput Biol 7 (2011), doi:10.1371/journal.pcbi.1001052↩ - [20]The advantage of considering the whole screen also comes from the mutual information in each moment.↩
- [21]Compare: “To measure the extent to which this information is integrated, we use the concept of effective information (φ), which refers to the information generated by the whole system, minus the information generated independently by the parts .” Anil K. Seth, Adam B. Barrett and Lionel Barnett, “Causal density and integrated information as measures of conscious level,” Phil. Trans. R. Soc. A 369 (2011): 3748–3767, doi:10.1098/rsta.2011.0079↩
- [22]To keep this demand within lower values, we can consider the decompositions in two parts only.↩
- [23]Cf. “Another feature of the IITC [information integration theory of consciousness, A/N] is that integrated information is identified with consciousness, implying a relation of sufficiency. In our view, dynamical complexity (information integration) may be necessary, but is unlikely to be sufficient for generating consciousness. A challenge to the IITC in this context is that all measures of integrated information so far described exhibit instabilities due to normalization, undermining the ascription of physical meaning to the quantity.”
Anil K. Seth, Adam B. Barrett, Lionel Barnett, “Causal density and integrated information as measures of conscious level,” Phil. Trans. R. Soc. A 369 (2011): 3748–3767, doi:10.1098/rsta.2011.0079
Cf. also Anil K. Seth, Eugene Izhikevich, George n. Reeke, and Gerald M. Edelman, “Theories and measures of consciousness: An extended framework.” PNAS 103 (2006): 10799-10804, doi: 10.1073/pnas.0604347103↩ - [24]John R. Searle, “Can Information Theory Explain Consciousness?” The New York Review of Books, January 10, 2013, http://www.nybooks.com/articles/archives/2013/jan/10/can-information-theory-explain-consciousness/
Christof Koch, Giulio Tononi, “Can a Photodiode Be Conscious?” The New York Review of Books, March 7, 2013, http://www.nybooks.com/articles/archives/2013/mar/07/can-photodiode-be-conscious/↩ - [25]John R. Searle, “Can Information Theory Explain Consciousness?” The New York Review of Books, January 10, 2013, http://www.nybooks.com/articles/archives/2013/jan/10/can-information-theory-explain-consciousness/↩
- [26]All the three citations in this paragraph come from Willard V.O. Quine, Word and Object (Cambridge: The MIT Press, 1960.) pp 90-91.↩
- [27]When we think about a lenght of code, we are using the word ‘code’ as a mass term, and we perceive it as a magnitude. Instead, when we talk of specific codes, we are using the word ‘code’ as general term. The logarithm leads us from the number of specific codes to the lengh of code needed to generate them. So, it happens that there is a bit of the logarithm in the relationship among code as mass term and code as general term.↩
- [28]According to Quine, substantive, adjective and verb can be viewed as “variant forms given to a general term.”↩